Listener Crossword 4869 Anagrams by Arden

by

Many thanks to LWO contributor Gill Cocks for this week’s Listener blog

Dear Arden,

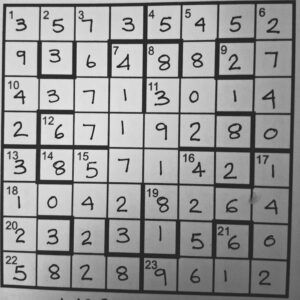
The construction was amazing – I cannot fathom how you would even start to put together a puzzle like Anagrams.

Solving it fell into 3 phases:

  1. Clever, and fun: realising that a difference of 1 meant that the only factors involved were 2 & 3, and that odd differences meant the lowest no was 2 and the highest was the difference+2. Only 2 ambiguities, 15dn & 16dn.
  2. Impossible, or at least requiring longer than I had between the date it landed and the deadline. Cue my husband’s ability to programme Mathematica to the rescue.
  3. Fast – there were only 3 possible solutions for 7dn, 2 for 12ac and a quick resolution when I fitted them with 8dn and 14ac.

What would have prolonged the fun for me would have been a sentence in the rubric to say “one of the 6-digit numbers is a famous cyclic example of the set of anagram multiples”. I might even have tried to solve it without recourse to Mathematica!

Now to find a wet towel and a darkened room,

Gill

Notes from Gill on how she did it:

  1. Only 2 primes have a difference of 1: 2 & 3
  2. If difference is odd, the smaller number is 2 and the largest is 2 + 2nd number
  3. 21dn 2 digits – 24 = 16; 34 = 81
  4. 18ac 210 = 1024
  5. 20ac 25 = 32; 35 too large
  6. 5dn 211 = 2048
  7. 9ac 24 x 3 = 48; 23 x 32 = 72; 22 x 33 = 108, too large
  8. 3dn 25 x 35 = 7776; 26 x 34 = 5184; 27 x 33 = 3456; 28 x 32 = 2304; 29 x 3 = 1536
  9. 17dn 74 = 2401
  10. 13dn must be 2, 1283. Other no is 2 to fit
  11. 4ac       2, 71, 23 = 3266; 2, 71, 37 = 5254 2nd 2 too small, 2nd 71 too big
  12. 6dn only pair that fits is 7, 601 therefore
    1. 9ac is 72
    2. 4ac is 5254
  13. 11ac 2, 13 and 2 out of 5, 7, 11 (2, 3 too small): 2, 5, 11, 13 = 1430
  14. 22ac    2, 1429 = 2858
  15. 23ac    only 9261 works
  16. 2dn      15 or 35

Now for the slog

  1. 19ac 5 candidates but only 4 consistent with 16dn: 1584, 3564, 5544, 8624
  2. 16dn 32 candidates; 3 consistent with 19ac & 23ac: 1612, 5642, 7502
  3. 15dn ends in 5 so must contain 5; 3 candidates 2275, 4225, 9295
  4. 1dn      18 candidates
  5. 10ac    8 candidates consistent with 3dn
    1. 1dn reduced to 12 candidates
    2. 10ac reduced to 6 candidates
    3. 3dn 5184 eliminated
  6. 1ac      3375 or 9375
    1. 2dn = 35
    2. 3dn = 7776
    3. 10ac = 4173
    4. 1dn = 3249 and 1ac = 3375
  7. 15dn (2275, 4225 or 9295) and 16dn (1612 or 5642) are ambiguous

Now for the bit that needs coding

  1. Each of the 6-digit anagram multiples in the first grid begins with 1, 2, 3 or 4
  2. Even so there are 1000s of possibilities; enter Mathematica to produce a list
  3. Given the constraints, there is only one answer for each of 7d, 8d, 12ac & 14ac
  4. 15dn and 16dn also resolve