Ah, we have the three-monthly numerical and it’s by Elap.
For better or worse, my solution is free from Mathematica and other online
programming solutions, although I did accept my husband’s offer of a list of possible
letter values which met the criteria stated in the rubric. Sometimes life is just too
short to create from scratch, whether it’s in the kitchen or in the study.
The gridfill was enjoyably straightforward and just required a clear head and
methodical approach. A line-by-line account of my not-quite-optimal steps is shown
at Appendix A; of course, there was much useful info to be derived from the crossing
numbers in the grid.
Deriving the message was the best part, possibly because I had already saved my
letter values in both numerical and alphabetical order. I guessed straight away that
reading the letters on a cut of 3 would be a good starting point, and the first word:
hInt confirmed that. So I had Hint: copy first numerals of cube.
Cube of what? The letter values? No, the rubric talked about the 33 3-digit entries,
so best use those. How many first numerals? Try 3, based on the title of the puzzle.
Like others I suspect, I tried 828 first but soon reached the end of the sequence.
After a few random stabs I derived the entire sequence, beginning in the bottom right
corner with 302. This is shown at Appendix B. This step was the least exciting but it
did give me 311 for 15ac and 207 for 18ac. Omitting those was a nice touch!
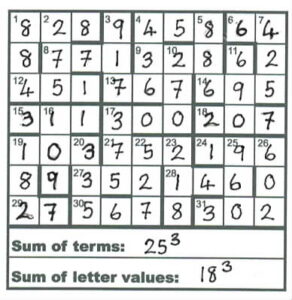
Summing the 33 terms and the 27 letter values however led to the delightful outcome
of two cubes: 25 3 and 18 3 respectively. These I have inserted below the grid.
Interestingly, my husband, who had used Mathematica to come up with the solution
the previous day (I had to make him promise not to tell me), favoured entering 156
and 583; as he pointed out, what did the rule say about cubes? Take the first 3 digits
…
Once again I am in awe of Elap’s imagination to come up with a new take on a
numerical; his innate knowledge that leads him to believe that such a construct is
even possible; the perseverance to find a sequence of cubes that is not only long
enough to fit in a grid but is sufficient to accommodate a carefully-crafted message of
length 3n letters; and, to cap it all, his ability to create the 33 clues which allow the
solution of the letter values with minimal redundancy.
A great bank holiday workout thanks Elap!
Appendix A to L4882 solution: the gridfill
6ac h = 4 64
29ac I = 5, 6, 9, 16, 21, 25 (from 8ac) I = 9; 29ac = 27
19ac 100-487 I = 5, 6, 9, 16, 21; (8ac) I = 9; a= 5 6 16 25 49 61 64 69 84 89 96
100
5dn 414-999 2L 2 + h; L = 16 – 22: 5dn = 516 or 886
5dn 886 L = 21
8ac 603 – 883 I 3 + 2L I = 9 771
3dn 887 – 917 h 2 S + L S = 56 3dn 917
9ac 118 – 448 h 2 I + u; u = 64 84 184 304 9ac 208 228 328 448
10dn 2xx or 4xx a 3 + aI; a = 6 10dn = 216 + 54 = 270
20dn 224 – 449 U-L U = 249 296 304 356 20dn = 228 275 283
335
30ac 501 – 599 begins with 5 (< 14ac)
20dn 335 U = 356
9ac 328 u = 184
22dn 501 – 599 a + y 6 + y; y = 521 561 569 22dn = 527 567 575
19ac 103 – 293 16 + 81 + 6 = 103
2dn 271 – 279 m – 21; m = 292 – 300 m = 296 2dn = 275
17ac 300 – 320 a 3 + C; 216 + C C = 84 17ac = 300
19dn 102 – 192 C + I + N; 93 + N N = 49 69 89 19dn = 142 162 182
4dn 430 – 539 2c + 4 c = 216 4dn = 436
30ac 505 – 597 21 + n + y ends in 5 or 7; 542 + n 582 + n 590 + n n = 5 25
7dn 405 – 497 ends in 5/7 i 2 + nR i = 5 n = 25 R = 16 7dn = 425
26dn 541 – 689 5/25 + 56 + 521/561/569 26dn = 582 602 622 630 642 650
11dn 542 – 698 10O O = 61 64 69 11dn = 610 640 690 (from 14ac)
14ac 611 – 699 126 + b b = 521 561 569 14ac = 647 687 695
28ac 105 – 181 in + 21 i = 5 25 n = 5 25 28ac =
146
31ac 302 – 322 6t – T t = 61 or higher
26dn 541 – 689 25 + 56 + 521/561/569 26dn = 602 642 650
14ac 647 – 695 ends in 5 14ac = 695 b = 569
13ac 767 6 + 569 + 2F F = 96
16dn 104 – 109 125 – R R = 16 16dn = 109
17dn 363 – 379 16t – f t = 49 61 64 69 f = 521 or bigger
12ac 450 – 559 5N + 6 N = 89 12ac = 451
4ac 458 – 498 96 + 178 +184 4ac = 458
30ac 545 – 597 21 + 25 + 521/561 30ac = 567 y = 521
22dn 527 – 567 6 + 521 22dn = 527
26dn 600 – 650 25 + 56 + 521 26dn = 602
11dn 690 10O O = 69
27ac 332 – 377 5 + p + 2s p = 1 49 61 64 100 216 249 304 s = 1 49 61 64
100
1ac 820 – 829 569 + 10 +p p = 249 1ac = 828
27ac 342 – 372 5 + 249 + 2s s = 49 27ac = 352
17dn 375 976 – f f = 601 649
25dn 860 – 969 6(r – f) f = 601 r = 761 25dn =
960
24ac 196 761 – e – 4 e = 561
31ac 302 6t – T t = 61 T = 64
21ac 752 601 + 2o – 49 o = 100
1dn 804 – 894 E + 184 – 64 E = 764 1dn = 884
19dn 162 – 182 93 + 89 19dn = 182
23dn 210 – 219 69 + 100 + 49 23dn = 218
Appendix B to L4882 solution: the gridfill
302-275-207-886-695-335-375-527-146-311-300-270-196-752-425-767-451-917-
771-458-960-884-690-328-352-436-828-567-182-602-218-103-109-[129]
I thought this was a superb puzzle, in my top three in a year which has provided many fine puzzles. An excellent grid construction, and what seemed like an almost magical end-game. Many thanks to Elap, and to Dash for the excellent blog.