Mr Snaky is back. His first Listener (4763) was about Pascal’s Theorem and it looks as we have more geometry this time too.
He also likes a pretty complex construction (which leads eventually to an elegant ending) and the preamble sets us up for one.
- Quite a lot of answers are too long for their spaces. Since the answer lengths are given we can see that these affect the perimeter
- which is further complicated because the perimeter entries have to be jumbled
- and then decoded using a substitution cipher.
- AND some normal clues have misprints in their definitions, spelling out a hint
After all that a thematic shape must be drawn using the diagonal from cell 1 and part of the top border, and the cell number highlighted that corresponds to its area.
‘Good luck!’ we thought as we ventured into the clues. The difficulty level was about average for the Listener, with some of the trickier clues using reversed phrases in the wordplay, so that e.g. 16a “Article following short fib (> fix) to the end (5) for ANNEX would to our mind more logically be “Article with short following” i.e. AN + NEX(t). But “following short” for “following shortened” now seems part of crossword grammar. It’s rather like the debate about “start” and “leader” and views will vary!
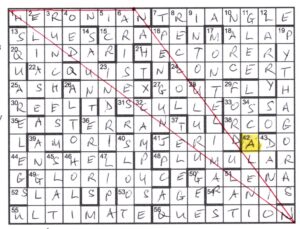 The DASH cleric enjoyed 13d “Portable seating affected church songs (10)” for CAMPCHAIRS and the other perimeter clues were similarly accessible which was a help when we faced the harder task of jumbling and then decoding them. The requirement that ‘real words’ be left was very helpful as it meant that alongside the encrypted jumble we could enter some letters or groups of letters of the plain text and use a dictionary app to generate candidate plain text words, the final set being HERONIAN TRIANGLE / PYTHAGORAS / ULTIMATE QUESTION / SQUARE LEGS, with the clue message ALEXANDRIAN MATHS ICON setting us off with HERO[N] (once we had explored HYPATIA and not got anywhere helpful).
The DASH cleric enjoyed 13d “Portable seating affected church songs (10)” for CAMPCHAIRS and the other perimeter clues were similarly accessible which was a help when we faced the harder task of jumbling and then decoding them. The requirement that ‘real words’ be left was very helpful as it meant that alongside the encrypted jumble we could enter some letters or groups of letters of the plain text and use a dictionary app to generate candidate plain text words, the final set being HERONIAN TRIANGLE / PYTHAGORAS / ULTIMATE QUESTION / SQUARE LEGS, with the clue message ALEXANDRIAN MATHS ICON setting us off with HERO[N] (once we had explored HYPATIA and not got anywhere helpful).
A Heronian Triangle is simply a scalene one with integer values for its sides, and it looked like that was what we were going to have to draw. Pythagoras suggested triangles too and specifically right-angled ones. To a Douglas Adams fan the Ultimate Question’s answer had to be 42, while Square Legs was presumably not an invitation to draw a cricket fielding layout but a reminder that the non-hypotenuse sides of a Pythagorean Triangle are usually called legs and are the sides of squares.
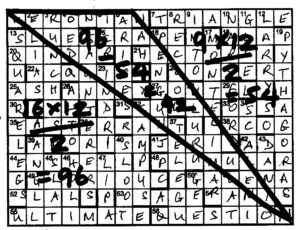 At this point it was back to head scratching and some pretty scratchy attempts at Geometry, but – guided by the lines given in the preamble – the idea soon formed of not getting the scalene triangular area of 42 directly but by subtracting the area of one right triangle from another, and 16*12/2 – 9*12/2 = 96 – 54 = 42. A picture is worth a thousand words:
At this point it was back to head scratching and some pretty scratchy attempts at Geometry, but – guided by the lines given in the preamble – the idea soon formed of not getting the scalene triangular area of 42 directly but by subtracting the area of one right triangle from another, and 16*12/2 – 9*12/2 = 96 – 54 = 42. A picture is worth a thousand words:
Not forgetting to highlight cell 42, this gave us our finished grid, with many thanks to Mr Snaky for the workout, with not much to go on to keep the Oenophile Club membership live, but perhaps the “counter measure” in 30 is an optic, and double brandies all round will do nicely.
I am no Terry Pratchett expert, but I thought the original exponent of 42 as the answer to the Ultimate Question was Douglas Adams in the Hitchhiker’s Guide to the Galaxy.
Whoops! Corrected! Always good to know the blog is being read…. Vagans